CV・CG・ロボティクスのためのリー群・リー代数入門: (1) リー群
このエントリでは,回転を題材としてリー群の定義を説明し,それを導入する動機と基本的な考え方を導入する.
ざっくりと言うと,回転を考えるというのはある種の「曲がった空間」を考えることであって,理論上も実用上も面倒な点が多い.ところがここで,回転が「群」と呼ばれる数学的構造を持っていることに着目すると,さっきの「曲がった空間」に関する問題を,それに対応する「真っ直ぐな空間」に関する問題に置き換えて考えることができる.ここで言う「曲がった空間」がリー群であり,「真っ直ぐな空間」がリー代数と呼ばれるものであり,それらの間の対応を表すのが指数写像と呼ばれるものである,という話をこのエントリとそれに続く 2 エントリくらいを通じて見ていきたい.
何やら魔法のような話に聞こえるかもしれないが,こんな風に,ある問題をそれと対応関係にある別の問題に置き換えて考えるというのは数学ではよくある話である.例えば,幾何学の問題を方程式の問題に置き換えて解くとか,線形微分方程式をラプラス変換して代数方程式に置き換えて解くなんてのは常套手段なわけで,似たようなものだと思えばそれほど恐れることもないと言える,かも知れない.
3 次元回転行列
まず,3 次元回転行列について基本的な事項をまとめておく.線形代数の復習なので,よくわかっている人は次の節までスキップして欲しい.
点の 3 次元位置を表す 3 次元ベクトル $\v{v}$ に $3 \times 3$ 行列 $\m{R}$ を左からかけて
$$
\begin{align}
\v{v}' &= \m{R} \v{v}
\end{align}
$$ とすることで,原点まわりの回転を表現することを考える.
回転前のベクトル $\v{v}$ として単位ベクトル $(1, 0, 0)\trans$,$(0, 1, 0)\trans$,$(0, 0, 1)\trans$ を与えたとすると,回転後の $\v{v}'$ は,$\m{R}$ の各列 $\v{r}_1$,$\v{r}_2$,$\v{r}_3$ にそれぞれ一致することがわかる.したがって,各列ベクトル $\v{r}_i$ のノルムは 1 であり ($\v{r}_i\trans \v{r}_j = 1$ if $i = j$),かつ互いに直交している ($\v{r}_i\trans \v{r}_j = 0$ if $i \neq j$).このことを行列として表示すると,単位行列 $\m{I}$ を使って
$$
\begin{align}
\m{R}\trans \m{R} &= \m{I}
\end{align}
$$ と書ける.このような行列 $\m{R}$ を直交行列と呼ぶ (意味的には正規直交行列と呼ぶ方がよさそうな気がするのだが,伝統的に直交行列と呼ばれる).
直交行列は回転を表すとは限らない.右手系が左手系に写ってしまうような鏡映が含まれる場合があるからである.これらを区別するには行列式をチェックすればよい.回転行列 $\m{R}$ の行列式 $| \m{R} |$ は $1$ である.なぜならば,行列式というのは,座標変換前後の符号つき体積拡大率を表すものであって,右手系と左手系が入れ替わるときに符号は負,そうでないときに正とすると約束するからである.回転でも鏡映でも体積は変わらないので拡大率は $1$ または $-1$ であり,特に回転では右手系と左手系が入れ替わることはないので,正符号である.結局,以下の定義に至る.
2 つの回転の合成は,行列の積によって表せる.何も動かない恒等変換 (これも回転の特殊例) は単位行列 $\m{I}$ で表される.
逆変換は逆行列 $\m{R}\inv$ をかけることで行えるが,直交行列の場合は,逆行列は転置行列に一致する.このことは $\m{R}\trans \m{R} = \m{I}$ の両辺に右から $\m{R}\inv$ をかけると $\m{R}\trans = \m{R}\inv$ となることからわかる.
群
さてようやく本題に入ろう.
リー群とは何かを述べる前に,群とは何なのかを回転を例にして考える.
前節で述べたとおり,回転は行列積によって合成できる.重要なのは,合成された結果もまた回転であり,例えば並進運動が現れたり対象物の形が変わるよな変換になったりは絶対しない.このことを指して「回転の集合は積について閉じている」という言い方をする.回転の積には以下のような性質がある.
- 3 つの回転を合成するとき,$(\m{R}_3 \m{R}_2) \m{R}_1$ の順で結合しても $\m{R}_3 (\m{R}_2 \m{R}_1)$ の順で結合しても結果は変わらない
- ある回転の効果を打ち消す操作 (すなわち $\m{R}$ に対する $\m{R}\inv = \m{R}\trans$) もやっぱり回転である
- 何もしない操作 (すなわち単位行列 $\m{I}$) も回転の一種である
このような性質を持つ集合,すなわち,結合則が成り立つ積という演算に関して閉じており,逆元と単位元がある集合のことを群と呼ぶ.
群の作用
ちょっと注意しておきたいのは,上の定義で考えている積というのは $\m{R}_2 \m{R}_1$ のことであって $\m{R} \v{v}$ のことではないという点である.前者は回転どうしの合成であり,後者は回転をベクトルに作用させる操作である.
回転の例に限らず一般に,群というものは,その元を他の対象に「作用させる」使い方をするものが多い.ところが,上で見た群の定義には,それが他の対象へどのように作用するかという概念は出てこない.
群の概念は,もともとはこのような「何かに作用するもの」として考えられてきたものだが,数学の議論が抽象化されていく過程で,作用とは切り離されて定義されるようになった.しかし,定義に現れないからといって作用の概念がなくなったわけではなく,群に関する考察の対象としては依然として重要なものである.
もう一つ注意しておくと,回転行列がベクトルに作用するときは $\m{R} \v{v}$ のように左からの乗算として作用するが,作用は必ずしもこの形に限らない.例えば,ある群の元である行列 $\m{G}$ が別の行列 $\m{X}$ に $\m{G} \v{X} \m{G}\inv$ のように作用して別な行列を作る,などというのも作用の一種であり,共役作用などと呼ばれる.後に見る四元数 (クォータニオン) による回転などはこの例である.
リー群
回転などの連続的な座標変換群は,さらに「なめらかな構造」を持つ群であることが特徴である.
具体的なイメージを描いてみよう.3 次元ベクトルの線形変換は $3 \times 3$ 行列で表せるので,9 次元実ユークリッド空間 $\mathbb{R}^9$ の 1 点に対応させることができる.具体的な表示としては $3 \times 3$ 個の要素を適当な順序で並べたベクトルを想定すればよい.
ここで,何らかの座標変換で 1 自由度のパラメータで表せるもの,例えばある軸まわりの回転を考えて,回転角度パラメータ $\theta$ を連続的に変化させるとすると,$3 \times 3$ 行列の各要素もやはり連続的に変化し,9 次元空間内の点はなめらかな曲線を描いて動く.同様に 3 次元回転変換全体の集合は,3 自由度で動くことになるので,その 9 次元空間内に 3 次元的に広がっていることになる.
「$n$ 次元的に広がっている」というのは,真面目な用語で言うと $n$ 次元の多様体であるという意味で,要は任意の点のまわりで局所的には $n$ 次元の座標を入れることができるような集合のことである.といっても高次元なものはどうせ想像できないので (個人の感想です),絵としては 3 次元空間に 2 次元曲面が広がっているところを想像しておけばよかろう.例えばこんな感じ.

この図は,とある 3 つのパラメータを使って 3 次元回転を表示して,そのうち 2 パラメータを自由に動かしながら,回転行列の (1, 3) 要素,(2, 3) 要素,(3, 3) 要素の値を x y z 座標だと思ってプロットしてみたものである.パラメータに対して各要素がなめらかに変化するから,なめらかな曲面が得られる.
念のため再確認しておくと,この図は 9 次元空間のうち 6 個の次元を潰して表示しており,また 3 次元の「超曲面」のうち 1 個の次元を潰して 2 次元曲面として表示していることに注意したい.何も考えずに低次元化した可視化なので,この図が群としての構造をうまく反映している保証は全く無いが,こんな感じのイメージをまずは持とう.
こういうなめらかな構造を持つ群をリー群と呼ぶ.もちろん本来は「なめらかとは何ぞや」という議論をする必要があり,そのためには位相とは,多様体とは,微分可能性とはといった話に突入しなくてはならないのだが,大変なのでばっさり略.上のような図ですべて察してもらうことにする.
コンピュータビジョン,グラフィクス,ロボティクスなどの分野で多用される座標変換は,その多くがリー群としての要件を満たす.回転のほかには,ユークリッド変換 (剛体変換),相似変換,アフィン変換などが挙げられるが,相似変換やアフィン変換からは「図形がつぶれて面積や体積が 0 になるような変換」は除外して考えないといけない.逆元の存在が保証できなくなるからである.一方,例えば 3 次元空間から 2 次元カメラ画像への投影変換のように次元が落ちる写像は,もちろんリー群に (というか群に) はならない.
接空間
曲面上の問題は,平面上の問題と比べて一般に扱いが難しい.例えば計測データをもとに物体の姿勢推定をしようとする場合,計測点が物体モデルに最もフィットするような座標変換を探す問題としてよく定式化されるが,そのような探索を曲面に沿って行わなくてはならず,厄介である.
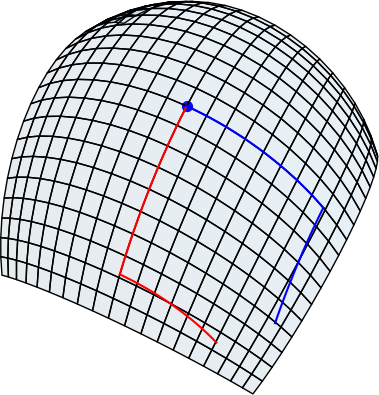
「曲がった空間」であることの厄介さの別の典型例を挙げておく.下の図は,x 軸まわりに 45 度回転した後に y 軸まわりに 45 度回転した場合のさっきの曲面上の経路を赤色で,同じことを先に y 軸まわり,続いて x 軸まわりの順に行った場合を青色で描いたものである.図からも,あるいは経験的にもわかるように,これらの操作は同じ結果にならない.この事実を指して,3 次元回転の群は非可換であると言ったりする.これも曲面上の探索やパラメータ表示を面倒にする要因になっている.
そこで,曲面の代わりに平面を使えないだろうか,ということを考える.

この図は,単位元 (つまり単位行列 $\m{I}$) に対応する点でさっきの曲面に接するような平面をプロットしてみたものである.曲面上を探索する代わりに,この平面上を動き回ることで済ませるならば,話はずいぶん楽になる.
「あー,はいはい,線形近似ってことでしょ.接点に十分近いところでないと誤差がどんどん大きくなるから,大きな回転は扱えないじゃん」
と思ったかもしれない.単に平面上を動き回るだけならその通りである.しかし,この平面上の各点から,近似ではなく常に厳密に,元の曲面の上に飛び移れるような「写像」が存在したとしたらどうだろう.平面上を動き回ることは曲面上を動き回ることの代用になるのではないか.
そのような写像の存在を探る前に,今描いてみた「平面」をもう少し真面目に定義しておこう.曲面に沿って,その上のある点 A を通る任意の曲線を考える.

曲線上を点が動いて A を通過する瞬間の速度ベクトル (青い矢印) を,A における接ベクトルと呼ぶ.同じ曲線でも点の動く速さが違えば速度ベクトルの大きさは異なるだろうが,その向きは同じである.A を通るあらゆる曲線のあらゆる速度についてこれを考えたときに,そのあらゆる接ベクトルの全体を A における接空間と呼ぶ.さっきの例は,単位元 $\m{I}$ における接空間である.
いくつか注意しておく.まずここでいう「ベクトル」とはどんなものかというと,今 3 次元回転を考えているのだとしたら,$3 \times 3$ 行列の要素を 1 列に並べた 9 次元ベクトルである.…のだが,いちいち「1 列に並べる」操作に言及していると大変なので,行列のまま「ベクトルである」と考えてしまうことが多い.同じサイズの行列の集合は,和とスカラ倍について閉じていてベクトル空間の公理を満たすので,数学的にはこう考えることに何の問題もない.
次に,接空間を「あらゆる接ベクトルの全体」と定義したときに,接ベクトルの始点はすべて原点に揃えて考えているということに注意したい.図の上では,便宜上,接点を通るような平面の絵を描くことが多いが,本当は接点が原点に来るように平行移動したものを考えている.
リー群と接空間の関係 ― 1 軸回転の場合
さて,以上のような定義のもとで,リー群の接空間から元のリー群にうつれるような便利な写像を見出すことができるかを探っていく.一般論のままでは難しいので,具体例として,2 次元平面内の回転,あるいは同じことだが,3 次元空間での 1 本の固定軸まわりの回転を考えてみることにする.これもリー群の一種である.
角度 $\theta$ だけ回転するような回転行列を $\m{R}(\theta)$ と書くことにする.平面回転の場合は $2 \times 2$ 行列で,空間回転の場合は $3 \times 3$ 行列だが,以降の話はそのどちらの場合でもよい.
$\m{R}(\theta)$ を $\theta$ で微分することを考える.微分の定義から
$$
\begin{align}
\frac{d\m{R}(\theta)}{d\theta} &=
\lim_{\delta\theta \rightarrow 0} \frac{\m{R}(\theta + \delta\theta) - \m{R}(\theta)}{\delta\theta}
\end{align}
$$ であるが,ここで 1 軸まわりの角度 $\theta + \delta\theta$ の回転は角度 $\theta$ の回転と角度 $\delta\theta$ の回転の合成であり,また $\m{R}(0) = \m{I}$ であることに注意すると
$$
\begin{align}
\frac{d\m{R}(\theta)}{d\theta} &=
\lim_{\delta\theta \rightarrow 0} \frac{\m{R}(\delta\theta)\m{R}(\theta) - \m{R}(\theta)}{\delta\theta}\\
&= \lim_{\delta\theta \rightarrow 0} \frac{\m{R}(\delta\theta) - \m{R}(0)}{\delta\theta} \m{R}(\theta)\\
&= \left. \frac{d\m{R}(\theta)}{d\theta} \right|_{\theta = 0} \m{R}(\theta)
\end{align}
$$ となる.
$\displaystyle \left. \frac{d\m{R}(\theta)}{d\theta} \right|_{\theta = 0}$ は $\m{R}(\theta)$ の各要素を $\theta$ で微分してから $\theta = 0$ を代入して得られる定数値行列である.これを $\m{X}$ と書くことにすると,$\m{R}(\theta)$ は
$$
\begin{align}
\frac{d\m{R}(\theta)}{d\theta} &= \m{X} \m{R}(\theta)\\
\m{R}(0) &= \m{I}
\end{align}
$$ という微分方程式に従うものだということがわかる.
この式は,(行列であることをいったん忘れると) 微分方程式としてはおなじみの形式をしている.
$$
\begin{align}
\frac{dz(t)}{dt} &= \alpha z(t)\\
z(0) &= 1
\end{align}
$$ の解が指数関数 $z(t) = \exp{\alpha t}$ であるというのはよく知られていることだろう.解き方 (定番は変数分離法) がすぐに思いつかない場合でも,この解を代入してみれば確かに与えられた微分方程式を満たしていることは簡単に確認できる.
同様に,さっきの行列微分方程式の解は,行列指数関数 $\exp{\theta \m{X}}$ なるもので与えられる.行列指数関数の定義については次回のエントリで説明するが,未習の人もこの場では「さっきの行列微分方程式の解を $\exp{\theta \m{X}}$ と定義する」と考えてしまって,そういうものが存在することを認めてしまおう.その上でこの節の話を振り返ると,以下のことがわかる.
- $\m{R}(\theta)$ は 1 軸まわりの回転を表す行列の群の上をパラメータ $\theta$ によって動く点であり,$\displaystyle \m{X} = \left. \frac{d\m{R}(\theta)}{d\theta} \right|_{\theta = 0}$ はその単位元 $\m{R}(0) = \m{I}$ における接ベクトルの一つである.
- 1 軸まわりの回転はそもそも 1 自由度しか持たないので,「単位元におけるあらゆる接ベクトル」とは「$\m{X}$ のあらゆる実数倍」のことである.つまり, $\theta$ が実数全体を動き尽くすとき,$\theta \m{X}$ は接空間全体を動き尽くす.
- 行列指数関数 $\exp(\cdot)$ は $\theta \m{X}$ の集合を 1 軸まわりの回転行列の群に写像する.
つまり,この節の冒頭で述べた「リー群の接空間から元のリー群にうつれるような便利な写像」は,1 軸回転群の場合は,行列指数関数によって与えられることがわかった.この「便利な写像」のことを指数写像と呼ぶ.
実はこのことは 1 軸回転群に限らずリー群全般について言えて,それゆえ「リー群の単位元における接空間」のことを,そのリー群に付随するリー代数と呼ぶ.そういう一般の場合について示すのを当面の目標 (具体的には次々回のエントリ) とする.