CV・CG・ロボティクスのためのリー群・リー代数入門: (3) リー代数
前回までに，1 軸回転群を例として，指数写像によって 1 軸回転群の中にうつることができるような「真っ直ぐな空間」を見出すことができて，それは単位元における接空間になっていることを見た．
このエントリでは，それが一般の行列リー群の場合にも見出すことができることを見ていく．その「真っ直ぐな空間」こそがリー代数と呼ばれるものなのだが，教科書を読んでいると大別して 3 つの異なる定義が出てくる．
- 指数写像による定義
- 接空間としての定義
- 抽象代数としての定義
最初の 2 つはこれまで 1 軸回転群を例として見たことの一般化である．以降でこれらが等価であることを見ていく．
3 つめの定義はちょっととっつきにくい．最初の 2 つはまず何らかのリー群を考えて，それに付随するリー代数を定義するものになっている．これに対して 3 つめは，まず先にリー代数を定義して，それが付随するようなリー群を見出すといった論法になっている．
以下ではこれらを順番に見ていく．
指数写像による定義
1 軸回転群の場合，任意の実数 $\theta$ に対して $\exp \theta \m{X}$ が回転行列を与えるような $\m{X}$ を見出すことができた．これにならって，以下のようにリー代数を定義する．これが第 1 の定義である．
リー代数の定義 (指数写像による定義)
あるリー群 $G$ が与えられたとき，あらゆる実数 $t$ に対して $\exp t\m{X} \in G$ となるような $\m{X}$ の集合を $G$ に付随するリー代数と呼ぶ．
「付随する」の代わりに「対応する」と表現することもあるが同じことである．リー群を $G$ と書くとき，それに付随するリー代数は $\mathfrak{g}$ と表す．リー群を表すときは英大文字を使い，それに付随するリー代数は同じ文字のドイツ小文字を使うのがだいたい慣例となっている．
この定義にあてはまるような $\m{X}$ の集合が見出せるなら，そのような任意の $\m{X}$ は指数写像によって $G$ の中にうつるのは定義から当然である ($t = 1$ とすればよい)．一方，そのような $\m{X}$ からなる空間は「真っ直ぐ」なものであって欲しいというのが我々の期待だったが，そうなることは以下のようにして見ることができる．
何らかのリー群 $G$ とそのリー代数 $\mathfrak{g}$ について，適当な $\m{X} \in \mathfrak{g}$ を用いて実数パラメータ $t$ によって描かれる曲線
$$
\begin{align}
\m{A}(t) &= \exp t\m{X}
\end{align}
$$ を考える．$t = 0$ のときは $\m{A}(0) = \m{I}$ つまり $G$ の単位元上にいる．$t$ とともに $\m{A}(t)$ がどう変わるかは $\m{X}$ に依存するが，$\mathfrak{g}$ の定義から $\m{A}(t)$ は曲面 $G$ 上から外れずに連続的に変化する．つまり $\m{A}(t)$ は，$\m{I}$ を通る $G$ 上の曲線になる．
$\m{A}(t)$ の $t = 0$ における微分は $\frac{d}{dt} \m{A}(t) |_{t = 0} = \m{X}$ であり，これは $G$ の $\m{I}$ における接ベクトルの 1 つである．
(「ん? 行列なのに接ベクトルとはどういうことだ?」と思った人は (1) リー群 を読み直そう．行列の要素を 1 列に並べたものをベクトルと同一視しているのだった)
$\m{X} \in \mathfrak{g}$ を自由に取り直しても，それは必ず接ベクトルになる．$\m{X}$ をいろいろ変えることでいろんな方向の接ベクトルが作り出せる．それらすべてからなる集合は，つまり指数写像によって定義した $\mathfrak{g}$ は，$G$ の $\m{I}$ における接空間という「真っ直ぐな空間」であることがわかる．
具体例: $SO(3)$ と $\mathfrak{so}(3)$
抽象的な話が続いたので，具体例として 3 次元回転の群を見ていくことにする．「3次元回転群」と呼び続けてもよいのだが，この分野の慣例に従って 3 次特殊直交群と呼ぶことにする．
「直交群」というのは直交行列からなる群だということであって，「3 次」とはそれが $3 \times 3$ 行列であることを表す．「特殊」というのは行列式が 1 の場合につく接頭語である．Special Orthogonal Group を略して $SO(3)$ と書く．数式で書くと
$$
\begin{align}
SO(3) &= \{\, \m{R} \in \mathcal{M}_{3}(\mathbb{R}) \mid \m{R}\trans \m{R} = \m{I}, |\m{R}| = 1 \,\}
\end{align}
$$ と定義することになる．念のためこの式の読み方を書いておくと，実数 $\mathbb{R}$ を要素とする $3 \times 3$ 行列 $\mathcal{M}_{3}(\mathbb{R})$ のうち，条件 $\m{R}\trans \m{R} = \m{I}$ と $ |\m{R}| = 1$ を満たすものの集合，ということである．
これに付随するリー代数 $\mathfrak{so}(3)$ を具体的に定めてみよう．任意の $\m{X} \in \mathfrak{so}(3)$ と実数 $t$ に対して $\exp t \m{X} \in SO(3)$ でなくてはならないから
$$
\begin{align}
\exp(t \m{X})\trans \exp(t \m{X}) &= \exp(t \m{X}\trans) \exp(t \m{X}) = \m{I}
\end{align}
$$ であることが要求される (行列指数関数は転置を保存することを使った)．両辺を $t$ で微分すると，行列積の微分の公式から
$$
\begin{align}
\left(\frac{d}{dt}\exp(t \m{X}\trans)\right) \exp(t \m{X}) + \exp(t \m{X})\trans \frac{d}{dt} \exp(t \m{X}) &= O
\end{align}
$$ であり，微分の計算を進めると
$$
\begin{align}
\m{X}\trans \exp(t \m{X}\trans) \exp(t \m{X}) + \exp(t \m{X})\trans \m{X} \exp(t \m{X}) &= O
\end{align}
$$ となる．特に $t = 0$ でもこれが成り立つ必要があることから，
$$
\begin{align}
\m{X}\trans + \m{X} &= O
\end{align}
$$ が要請される．この条件 $\m{X}\trans = - \m{X}$ を満たす行列は歪対称行列あるいは交代行列などと呼ばれる．
さらに
$$
\begin{align}
| \exp(t \m{X}) | &= 1
\end{align}
$$ でなくてはならず，行列指数関数の行列式の公式からこれは $\exp(t \tr \m{X}) = 1$ を意味する．$t \tr \m{X} = 0$ が任意の $t$ について成り立つ必要があるので
$$
\begin{align}
\tr \m{X} &= 0
\end{align}
$$ でなくてはならない．
逆に，この 2 つの条件 $\m{X}\trans = - \m{X}$ と $\tr \m{X} = 0$ を満たす任意の $\m{X}$ は，
$$
\begin{align}
(\exp t \m{X})\trans \, \exp t \m{X} &= \exp t \m{X}\trans \, \exp t \m{X}\\
&= \exp (- t \m{X})\, \exp t \m{X}\\
&= \exp (-t \m{X} + t \m{X}) \,\,\,(\text{∵ $-\m{X}$ と $\m{X}$ は可換})\\
&= \m{I}
\end{align}
$$ を満たし，かつ
$$
\begin{align}
|\exp t \m{X}| &= \exp (\tr t \m{X}) = \exp 0 = 1
\end{align}
$$ を満たすので，確かにこれが $\m{X} \in \mathfrak{so}(3)$ であるための条件であることがわかる．すなわち
$$
\begin{align}
\mathfrak{so}(3) &= \{\, \m{X} \in \mathcal{M}_{3}(\mathbb{R}) \mid \m{X}\trans = - \m{X}, \tr \m{X} = 0 \,\}
\end{align}
$$ である．
歪対称でトレースが 0 という条件は 1 次式で表されるので，この集合は「真っ直ぐな空間」であると言える．もう少し具体的に見てみると，
$$
\begin{align}
\m{X} &= \bmat
x_{11} & x_{12} & x_{13} \\
x_{21} & x_{22} & x_{23} \\
x_{31} & x_{32} & x_{33} \\
\emat
\end{align}
$$ と書いたとき，$\m{X}\trans = -\m{X}$ より
$$
\begin{align}
x_{12} &= - x_{21}\\
x_{31} &= - x_{13}\\
x_{23} &= - x_{32}\\
x_{11} &= - x_{11} \,\,\,\text{ すなわち }\,\, x_{11} = 0\\
x_{22} &= - x_{22} \,\,\,\text{ すなわち }\,\, x_{22} = 0\\
x_{33} &= - x_{33} \,\,\,\text{ すなわち }\,\, x_{33} = 0
\end{align}
$$ が要求される．$\tr \m{X} = 0$ より
$$
\begin{align}
x_{11} + x_{22} + x_{33} &= 0
\end{align}
$$ も要求されるが，これは上の条件に含まれる．
結局 $\m{X}$ の 9 つの要素のうち自由に変えられるのは 3 つだけなので，改めて $x_1 = x_{32}, x_2 = x_{13}, x_3 = x_{21}$ と置いて
$$
\begin{align}
\m{X} &= \bmat
0 & -x_3 & x_2 \\
x_3 & 0 & -x_1 \\
-x_2 & x_1 & 0 \\
\emat
\end{align}
$$ と表すことにする．ここで
$$
\begin{align}
\m{J}_1 = \bmat
0 & 0 & 0 \\
0 & 0 & -1 \\
0 & 1 & 0 \\
\emat, \,\,
\m{J}_2 = \bmat
0 & 0 & 1 \\
0 & 0 & 0 \\
-1 & 0 & 0 \\
\emat, \,\,
\m{J}_3 &= \bmat
0 & -1 & 0 \\
1 & 0 & 0 \\
0 & 0 & 0 \\
\emat
\end{align}
$$ を導入すると，
$$
\begin{align}
\m{X} &= x_1 \m{J}_1 + x_2 \m{J}_2 + x_3 \m{J}_3
\end{align}
$$ と書ける．
つまり任意の $\m{X} \in \mathfrak{so}(3)$ は，$\m{J}_1$，$\m{J}_2$，$\m{J}_3$ の線形結合として一意に表されるということであり，すなわち $\mathfrak{so}(3)$ は $\m{J}_1$，$\m{J}_2$，$\m{J}_3$ を基底とする 3 次元ベクトル空間である．これが「真っ直ぐ」であることの具体的な意味である．
接空間としての定義
前節では，指数写像によってリー代数を定義して，それがリー群の接空間になることを示した．今度はその逆を見ていくことにする．つまり，リー代数の第 2 の定義として，
と定める．この定義のもとで，その任意の元が指数写像によってリー群の中にうつることを見てみよう．
さらりと書いたが，これは実は驚くべきことである．前節のように，指数写像による対応関係という広域にわたる構造から単位元 1 点のみに着目した接空間の構造を導けるのはまあできそうだなと思えるのだが，今見ようとしているのはその逆である．単位元 1 点の構造のみによって「リー代数の任意の元とリー群の対応」というもっと広い範囲の構造が決まってしまうことを意味する．
リー群 $G$ の単位元における任意の接ベクトルを $\m{X}$ とする．これから示したいことは，このとき任意の実数 $t$ に対して $\exp t\m{X} \in G$ となることである．これを任意の $\m{X}$ と任意の $t$ について示すことが要求されているのだが，接ベクトルは実数倍しても接ベクトルなのだから，任意の接ベクトル $\m{X}$ について $\exp \m{X} \in G$ であることを示せば十分である．
まず $G$ の上の曲線 $\m{A}(t)$ で $t = 0$ における接ベクトルが $\m{X}$ となるものを適当に選ぶ．そのような曲線は
$$
\begin{align}
\m{A}(t) &= \m{I} + t\m{X} + O(t^2) + \cdots
\end{align}
$$ と表せる．ただし $O(t^2)$ は $t$ の 2 次以上の項を表す．下の図で，青い矢印が $\m{X}$，緑の曲線が $\m{A}(t)$ である．
ここで整数 $ m $ を用いて $t = 1/m$ に取り，それを $ m $ 乗した
$$
\begin{align}
\m{A}(1/m)^m &= (\m{I} + \frac{\m{X}}{m} + \epsilon)^m
\end{align}
$$ を考える．$\epsilon$ は $1/m$ の 2 次以上の項である．さっきの図でマゼンタ色で描かれているのは，折れ線 $\m{A}(1/m)^k$ ($k = 0, 1, \cdots, m - 1$) を $ m $ を増やしながらアニメーションさせたものである．
$\m{A}(1/m)$ は $G$ の元であり，$G$ は積について閉じているのだから，$\m{A}(1/m)^{m}$ も $G$ の元である．ここで $m \to \infty$ とすると，右辺は連続複利の公式から $\exp \m{X}$ に収束する．これが左辺と等しいので $\exp \m{X} \in G$ である．これが示したいことであった．さっきの図には赤色の曲線が描かれているが，実はこれは $\exp t\m{X}$ ($0 \leq t \leq 1$) を描画したものであり，確かに折れ線のアニメーションがここに収束していることがわかる．
以上の議論から，リー代数の「指数写像による定義」と「接空間としての定義」は互いに等価であるといってよい．以降ではそのときそのときで考えやすい方を使って考えることにする．
具体例: $SO(3)$ と $\mathfrak{so}(3)$
また 3 次元空間での回転を考える．
x 軸まわりに角度 $t$ だけ回転する回転行列は
$$
\begin{align}
\m{R}_x(t) &= \bmat
1 & 0 & 0 \\
0 & \cos t & -\sin t \\
0 & \sin t & \cos t \\
\emat
\end{align}
$$ である．これは $SO(3)$ の上をパラメータ $t$ とともに動く曲線であり，$t = 0$ で単位元 $\m{I}$ になる．$t = 0$ における微分は
$$
\begin{align}
\left. \frac{d}{dt} \m{R}_x(t) \right|_{t=0} &= \bmat
0 & 0 & 0 \\
0 & -\sin 0 & -\cos 0 \\
0 & \cos 0 & -\sin 0 \\
\emat\\
&= \bmat
0 & 0 & 0 \\
0 & 0 & -1 \\
0 & 1 & 0 \\
\emat
\end{align}
$$ であり，これは以前見た $\m{J}_1$ に一致する．同様に，y 軸まわり，z 軸まわりの回転を単位元において微分したものがそれぞれ $\m{J}_2, \m{J}_3$ に一致する．これらによって張られるのが接空間であり，したがって $\mathfrak{so}(3)$ である．
このように，どちらの定義から出発しても，リー代数としては同じものが得られることがわかる．
ベクトル空間の基底の取り方は無数にあるので，$\mathfrak{so}(3)$ の基底の取り方も $\m{J}_1, \m{J}_2, \m{J}_3$ には限らないのだが，このように x, y, z 各軸まわりの回転の微分というわかりやすい解釈ができることから，標準的に用いられるものとなっている．今後も $\m{J}_i$ という記号はこの意味で用いる．枠線で囲って再掲しておこう．
$\mathfrak{so}(3)$ の標準的な基底
$$
\begin{align}
\m{J}_1 = \bmat
0 & 0 & 0 \\
0 & 0 & -1 \\
0 & 1 & 0 \\
\emat, \,\,
\m{J}_2 = \bmat
0 & 0 & 1 \\
0 & 0 & 0 \\
-1 & 0 & 0 \\
\emat, \,\,
\m{J}_3 &= \bmat
0 & -1 & 0 \\
1 & 0 & 0 \\
0 & 0 & 0 \\
\emat
\end{align}
$$
リー代数の構造
リー代数 $\mathfrak{g}$ の原点 $\m{O}$ は指数写像によりリー群 $G$ の単位元 $\m{I}$ にうつる．$\mathfrak{g}$ 内で原点から引かれた任意の方向の直線は，指数写像によって $G$ 内で単位元から延びる曲線にうつされる．$\mathfrak{g}$ 内の直線をぐるりとあらゆる方向に取って考えると，指数写像は連続なので，$\mathfrak{g}$ のあらゆる元を指数写像でうつした像は $G$ の単位元の近傍を覆い尽くすことになる．
リー代数はベクトル空間だから，$\mathfrak{so}(3)$ の例で見たように適当な基底 $\m{X}_1, \m{X}_2, \cdots$ を取ることができ，任意の元をその線形結合で $\m{X} = a_1 \m{X}_1 + a_2 \m{X}_2 + \cdots$ のように表せる．この $(a_1, a_2, \cdots)\trans$ を $\m{X}$ を表すパラメータとして用いることができるし，その $\m{X}$ を指数写像でうつした先を表すパラメータとしても (指数写像が届く範囲内であれば) 用いることができる．リー代数の中に (したがって，少なくとも単位元近傍ならばリー群の中にも) 座標を入れられるということになる．
これまで図解に使ってきた曲面は，実は $\exp(t \m{J}_1 + s \m{J}_2)$ を実パラメータ $t$ と $s$ を動かしながら描画したもので，曲面上のグリッドは $t$ と $s$ を等間隔に取って描画したものだった．「座標を入れられる」の意味がわかってもらえるかと思う．
「ベクトル空間であること」はリー代数の重要な特徴だが，リー代数にはそれに加えて，交換子積と呼ばれる演算について閉じていることが要請される．交換子積は以下のように定義される．
交換子積の定義
$$
\begin{align}
[\m{X}, \m{Y}] &= \m{X}\m{Y} - \m{Y}\m{X}
\end{align}
$$
つまりリー代数 $\mathfrak{g}$ には，スカラ倍と和について閉じていなければならないというベクトル空間としての要請に加えて，$\m{X}, \m{Y} \in \mathfrak{g}$ ならば $[\m{X}, \m{Y}]$ も $\mathfrak{g}$ の元であることが必要となる．
この必要性は以下のように理解することができる．リー代数 $\mathfrak{g}$ の適当な 2 つの元 $\m{X}$，$\m{Y}$ を使って，実数 $t$ とともに動く曲線
$$
\begin{align}
\m{P}(t) &= \exp(t\m{X}) \exp(t\m{Y}) \exp(-t\m{X}) \exp(-t\m{Y})
\end{align}
$$ を考える．指数写像は常に $G$ の上にうつり $G$ は積について閉じているのだから，$\m{P}(t)$ は常にリー群 $G$ の上にある．
4 つの exp をそれぞれ 2 次の項まで展開し，$\m{X}$ と $\m{Y}$ は一般に可換ではないことに注意して整理すると，
$$
\begin{align}
\m{P}(t) &= (\m{I} + t\m{X} + \frac{t^2 \m{X}^2}{2} + \cdots) (\m{I} + t\m{Y} + \frac{t^2 \m{Y}^2}{2} + \cdots) (\m{I} - t\m{X} + \frac{t^2 \m{X}^2}{2} + \cdots) (\m{I} - t\m{Y} + \frac{t^2 \m{Y}^2}{2} + \cdots)\\
&= \m{I} + t^2 (\m{X}\m{Y} - \m{Y}\m{X}) + O(t^3)
\end{align}
$$ となる．$O(t^3)$ は $t$ の 3 次以上の項とする．$t$ の 1 次の項が現れないことに注意したい．
$\m{P}(t)$ は $t$ をパラメータとして $G$ 上を動く曲線だったが，ここで $s = t^2$ という新しいパラメータを取って，$s$ とともに動く $\m{Q}(s) = \m{P}(\sqrt{s})$ を新たに考える．$\m{Q}(s)$ の曲線としての形状は $\m{P}(t)$ の $t \geq 0$ の部分と同じである (パラメータによる進み具合が違うだけである)．したがってその $s = 0$ における接ベクトル
$$
\begin{align}
\left. \frac{d}{ds} \m{Q}(s) \right|_{s = 0} &= \m{X}\m{Y} - \m{Y}\m{X}
\end{align}
$$
は $G$ の接空間 $\mathfrak{g}$ に含まれていなければならない．よって $\mathfrak{g}$ が交換子積について閉じていることの必要性が示された．
$\m{P}(t)$ がどういう意味を持つのか，3 次元回転 $SO(3)$ を例として考えてみる．$\exp t\m{X}$ が x 軸まわりの $t$ rad の回転，$\exp t\m{Y}$ が y 軸まわりの $t$ rad の回転だとしよう．すると $\m{P}(1)$ は，y 軸まわりに $-1$ rad，x 軸まわりに $-1$ rad，y 軸まわりに $+1$ rad，x 軸まわりに $+1$ rad の順に回す操作を表す．やってみるとわかるのだが (といってもちょうど 1 rad 回すのは難しいので，例えば 90 度ずつ回してみることを考えるとよい)，この操作では元の姿勢 (つまり単位元) には戻らない．戻らない理由は $\m{X}$ と $\m{Y}$ が可換ではないからである．
曲面上に表示してみると下の図のようになる．青い矢印 2 本が $\m{X}$ と $\m{Y}$ の方向を表す．$t = 1$ [rad] の回転を 4 回行った軌道の先端の赤い丸は，元の位置である単位元 (青い丸) からずれている．
単位元からの「ずれ」の大きさは $t$ を変えると変化する．$t$ が 0 に近づくとだんだん小さくなり，$t = 0$ ではそもそも無回転を 4 つ合成するだけなので，ずれも無くなる．このように 4 つの回転を合成した結果が $t = 0$ から離れるとともに単位元からずれていく様子を $\m{P}(t)$ や $\m{Q}(s) $ は表しており，$t = 0$ においてずれ始める方向が $\m{X}\m{Y} - \m{Y}\m{X}$ である．この方向ベクトルも $\mathfrak{so}(3)$ に属していないと「4 つの回転を合成した結果が回転ではなくなる」といったおかしな事態が起きる．
交換子積の性質
後々の議論でよく使うので，交換子積が満たす重要な性質を挙げておく．
双線形性
$$
\begin{align}
[a_1 \m{X}_1 + a_2 \m{X}_2, \m{Y}] &= a_1 [\m{X}_1, \m{Y}] + a_2 [\m{X}_2, \m{Y}]\\
[\m{Y}, a_1 \m{X}_1 + a_2 \m{X}_2] &= a_1 [\m{Y}, \m{X}_1] + a_2 [\m{Y}, \m{X}_2]
\end{align}
$$
歪対称性
$$
\begin{align}
[\m{X}, \m{Y}] &= -[\m{Y}, \m{X}]
\end{align}
$$
これらは $[\m{X}, \m{Y}] = \m{X}\m{Y} - \m{Y}\m{X}$ を両辺に代入して展開することで簡単に示せる．
ヤコビの恒等式
$$
\begin{align}
[\m{X}, [\m{Y}, \m{Z}]] + [\m{Y}, [\m{Z}, \m{X}]] + [\m{Z}, [\m{X}, \m{Y}]] &= \m{O}
\end{align}
$$
一見して捉えにくい式だが，各項で $\m{X}, \m{Y}, \m{Z}$ がサイクリックに入れ替わっていることに着目するとよい．こちらも，ちょっと手間はかかるが同様に単純な計算で示せる．
交換子積の果たす役割
交換子積が必要であることはわかったが，「$t \to 0$ の極限で必要だから」と言われても，その重要性がどうもピンと来ないのではなかろうか．
交換子積がもっと本質的な役割を果たしていることを垣間見てみよう．そのために以下の公式を紹介する．
ベイカー・キャンベル・ハウスドルフの公式
$$
\begin{align}
\exp \m{X} \exp \m{Y} &=
\exp\left(\m{X} + \m{Y} + \frac{1}{2} [\m{X}, \m{Y}]
+ \frac{1}{12} [\m{X}, [\m{X}, \m{Y}]] - \frac{1}{12} [\m{Y}, [\m{X}, \m{Y}]] + \cdots \right)
\end{align}
$$
ここで $[\,\cdot\,, \,\cdot\,]$ が交換子積である．最後の $\cdots$ のところが略されており，項は無限に続くのだが，なんとすべて交換子積の組み合わせで書けることが知られている (書けるという事実だけではなく，具体的な式の形すら既に得られている)．証明は簡単ではないので省略するが，例えば帰納法 ($n$ 次までの項が交換子積の組み合わせで書けるなら，$n + 1$ 次の項も書けることを導く) によって示すことができる．収束は残念ながら無条件ではなく，$\m{X}$ と $\m{Y}$ が原点 $\m{O}$ に十分近くなくてはならない．
交換子積 $[\m{X}, \m{Y}] = \m{X}\m{Y} - \m{Y}\m{X}$ は，$\m{X}\m{Y}$ と $\m{Y}\m{X}$ がどのくらい異なるか，つまり，どのくらい強く非可換かを表す量であると見ることができる．$\m{X}$ と $\m{Y}$ が可換なら $[\m{X}, \m{Y}] = \m{O}$ であり，この公式は積法則 $\exp \m{X} \exp \m{Y} = \exp(\m{X} + \m{Y})$ に一致する．非可換のときは，その非可換さの度合いに応じて積法則から乖離していくが，$\m{X}$ と $\m{Y}$ が何らかのリー代数 $\mathfrak{g}$ に属しているならば，右辺の exp の中身もそのリー代数に属しているので，それを指数写像で飛ばした先がリー群 $G$ の中であることが保証される．
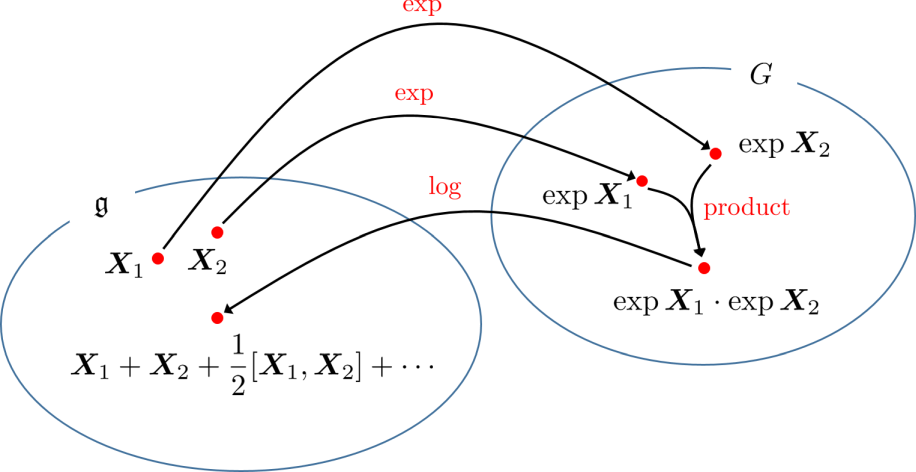
結局，交換子積について閉じていることは，リー代数とリー群が指数写像によって対応していることを (少なくともリー代数の原点近傍とリー群の単位群近傍において) 保証する役割を果たすと理解できる．
このような対応関係を利用することで，リー群に関する問題をリー代数の問題に置き換えて考えたりすることができる．リー群の構造というのは要するに，この元とあの元をかけるとどの元になるか (回転で言うなら，この回転とあの回転を合成するとどんな回転になるか) ということだが，元は無限にあるため，それらを調べつくすのは一般に容易なことではない．しかしその構造は，対応するリー代数のスカラ倍，和，交換子積の挙動によって，少なくとも単位元の近傍では完全に支配されている．
元が無限にあるのはリー代数だって同じだが，重要なのは，リー代数はベクトル空間だということである．よって，適当な基底を考えて，各基底ベクトルどうしの交換子積をすべて調べ上げておけば，あらゆる元の挙動がいつでも記述できる．本テキストで扱うリー代数は有限次元なので，基底ベクトルの数は有限である．リー群そのものを考えるよりはずっとやりやすい．
「そうは言っても単位元近傍だけなんでしょ?」という感想が出てくるのはもっともである．しかし，近傍ではあるものの，それが無限小の近傍ではなくて有限サイズの近傍であることが重要である．単位元近傍のあらゆる方向の小さな (しかし無限小ではない) 運動がいったん定まれば，それらを多数かけ合わせることでどんな大きな運動でも合成することができる．その意味で，単位元と連結した範囲にある元ならば，リー代数の十分に小さな元 $\m{X}_1, \m{X}_2, \m{X}_3, \cdots$ を使って $\exp(\m{X}_1) \cdot \exp(\m{X}_2) \cdot \exp(\m{X}_3) \cdots$ のように表せる．もう少し条件を限定すれば (具体的にはリー群に単連結性なるものを仮定すれば)，その表し方が一通りに定まることも知られている．
抽象リー代数
これまで，何らかのリー群から出発してそれに付随するリー代数を定義し，その性質を見てきたのだけど，その結果見えてきたことは，リー代数の構造によってリー群の (少なくとも単位元近傍の) 構造が支配されているということだった．
だったらリー代数から出発してもいいんじゃないの? というのは当然の発想であろう．
「交換子積の性質」の項で述べた双線形性，歪対称性，ヤコビの恒等式の 3 つが成り立つような「積」をリー括弧積 (あるいは単に括弧積) と呼ぶ．交換子積を抽象化したものと言える．そして，リー括弧積について閉じているベクトル空間のことをリー代数と定義する．これがリー代数の第 3 の定義である．
こうやってリー代数を定義してやると，それと対応するリー群が (少なくとも単位元近傍で) 定まって，これまで議論してきたような世界が構築される．
かくして数学の本ではこの定義が用いられることが多い．厳密で簡潔な論理展開がしやすいからである．一方，応用指向のユーザにとっては第 1 または第 2 の定義の方が把握しやすいのだが，第 3 の定義が現れる背景も知っておいた方が，理論屋さんが書いた文献を読むときについて行きやすくなるのではなかろうか (ついて行けるとは言ってない)．
リンク
